向量大小(Vector3长度.length())

本节课给大家介绍下向量长度(大小)的概念，并使用Three.js三维向量类Vector3的方法.length()计算向量长度，比如通过.length()计算3D空间中两点之间的距离。

为了让大家更容易理解向量长度的概念，更容易理解.length()方法，下面举一个具体的应用场景来讲解。

人从A点移动到B点移动

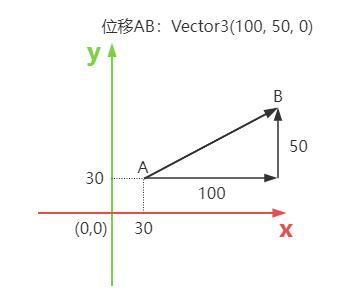
已知人在3D空间中，从A点移动到B点，A点坐标是(30,30,0)，B点坐标是(130,80,0)。

Vector3作为标量，表示人的起始点位置坐标。

const A = new THREE.Vector3(30,30,0);// 人起点A
const B = new THREE.Vector3(130,80,0);// 人运动结束点B

计算AB两点之间距离(初高中数学)

为什么在这里强调初高中数学，主要是因为总有学员咨询，自己数学基础不好，能学习threejs吗？入门的话，无所谓，进阶的话，如果数学基础很好，结合文档自学没啥压力，跟着课程更快点，如果数学基础不好，自学肯定比较困难，如果是跟着咱们系统课程数学进阶部分学习的话，会极大降低你学习难度和节约学习时间。

沿着A点绘制一条平行于x轴的直线，沿着B点绘制一条平行于y轴的直线，两条直线交叉点是O，AOB构成一个直角三角形。先不考虑z轴，三角形AOB位于XOY平面上。用你初中学过的勾股定理就可以计算出来AB线段的长度，也是人从A点移动B点的距离。

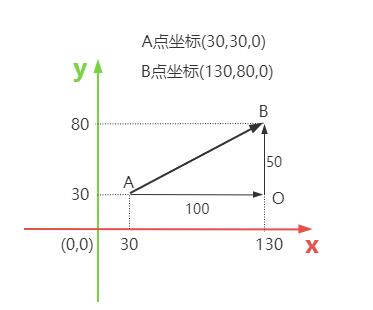
const x1 = A.x;
const x2 = B.x;
const y1 = A.y;
const y2 = B.y;
const AO = x2-x1;
const BO = y2-y1;
// 勾股定理计算三角形斜边长度(初中数学)
const L = Math.sqrt(AO*AO + BO*BO);
// 计算结果：50√5(111.803)
console.log('L',L);

把上面计算过程总结下，平面上两点距离计算公式

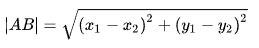
推广到三维空间考虑x、y、z三个分量，和2D平面上长度计算逻辑是一样的，下面是3D空间两点之间距离公式 (opens new window)(高中数学)

A和B两点的x、y、z分量分别相减，相减结果平方，然后相加，最后平方根，就是AB长度。

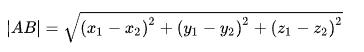
const A = new THREE.Vector3(30, 30, 0);// 人起点A
const B = new THREE.Vector3(130,80,0);// 人运动结束点B
// 3D空间，A和B两点之间的距离
const L = Math.sqrt(Math.pow(B.x-A.x,2) + Math.pow(B.y-A.y,2) + Math.pow(B.z-A.z,2));

向量Vector3表示位移量(A到B的移动)

从A点到B点的移动，可以用一个向量表示。

已知人在3D空间中的坐标A点是(30,30,0),此人运动到B点(130,80,0)，已知AB在x轴上投影长度是100，y方向投影长度是50，这个变化可以用三维向量THREE.Vector3(100,50,0)表示,换句话说，你也可以理解为人从A点开始，沿着x轴走了100，沿着y方向走了50，到达B点。

const A = new THREE.Vector3(30, 30, 0);
const B = new THREE.Vector3(130,80,0);
const AB = new THREE.Vector3();
AB.x = B.x-A.x;
AB.y = B.y-A.y;
AB.z = B.z-A.z;

向量减法运算.subVectors()

AB.subVectors(B,A);的含义表示B的xyz三个分量，与A的xyz三个分量分别相减，然后赋值给向量AB。

const A = new THREE.Vector3(30, 30, 0);
const B = new THREE.Vector3(130,80,0);
const AB = new THREE.Vector3();
AB.subVectors(B,A);

向量减法运算.sub()

B.sub(A);表示B的xyz三个属性分别减去A的xyz三个属性，然后结果赋值给B自身的xyz属性

B.sub(A);
console.log('B',B);

如果希望基于A和B两点位置，生成一个A指向B的向量，可以B克隆一个新对象，减去A。(如果B不克隆，B本身会被改变)

const AB = B.clone().sub(A);
console.log('AB',AB);

向量AB的物理含义

• 方向
• 长度(大小)

向量AB包含了两层信息，一个是从A移动到B点的位移方向，另一层信息是AB两点的距离，你可以把AB两点之间的距离称为向量长度(大小)。

总结：在该移动案例中，向量的长度就表示A和B两点之间的距离。

向量长度.length()

threejs的类Vector3的封装了一个方法.length()，用于计算向量长度。

向量长度.length()的内部代码，本质上就是x、y、z三个分量平方和的平方根。

const AB = B.clone().sub(A);
const L = AB.length();
console.log('L',L);

B.clone().sub(A)和AB.length()本质上表达的计算过程，就是上面介绍的两点之间的距离公式。.sub()表示了xyz分量分别相减，.length()表示相减结果，平方和的平方根。

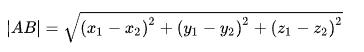
AB.length()计算的结果表示向量的长度，其实你对比下计算结果，就知道AB.length()计算的结果就表示A点到B点的距离。

两点之间距离计算总结

有了.sub()和.length()两个方法，两点之间距离计算，不需要自己写公式，直接用Threejs封装好的向量长度方法.length()即可，也就是用threejs封装好的方法简化计算代码。

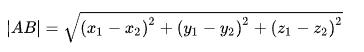
const A = new THREE.Vector3(30, 30, 0);
const B = new THREE.Vector3(130,80,0);
// 两点坐标构建一个向量AB
const AB = B.clone().sub(A);
// 向量长度表示AB两点距离
const L = AB.length();
console.log('L',L);

总结：向量分解为xyz三个方向

在三维空间中一个向量，使用Vector3()表示向量的规则，可以理解为一个向量在xyz三个轴上的投影长度。

一个人从A点移动到B点，移动距离是√2米，移动方向是x、y正半轴的角平分线。

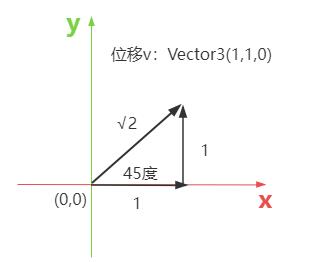
const AB = new THREE.Vector3(1,1,0);

总结：向量合成

已知Vector3(1,1,0)表示的位移向量，合成向量的方式比较简单，把多个xyz三个分量首尾相接。

const AB = new THREE.Vector3(1,1,0);

向量表示速度

刚刚咱们通过位移介绍了向量的大小，可以表示两点之间的距离。大家都知道向量不仅仅可以表示人或物体的位移，也可以表示速度、加速度、力等物理量。

下面以速度为例进一步介绍，向量的物理含义。

假设一个人的运动速度大小是√2,方向是x和y正半轴的角平分线，那么人的速度向量分解为xyz三个方向，可以用向量THREE.Vector3(1, 1, 0)表示。

const v = new THREE.Vector3(1, 1, 0);

速度向量长度.length()含义

已知人速度向量THREE.Vector3(1, 1, 0)，那么它的物理含义就是方向是x、y正半轴的角平分线，大小√2米每秒。

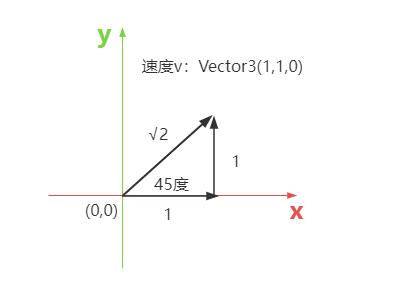
const v = new THREE.Vector3(1, 1, 0);

速度向量，包含人的方向信息，也包含人的速度快慢信息，如果想获取速度大小信息，可以通过向量长度方法.length()快速计算。

// v表示速度向量，v的长度.length()是就是速度的大小
const v = new THREE.Vector3(1, 1, 0);
const vL = v.length();
console.log('vL',vL);