threejs坐标系与三角函数

虽然大部分同学对three.js的坐标系和三角函数已经很熟悉了，但是这是threejs空间几何计算比较重要的内容，有必要在讲解一遍。

如果你特别熟悉了，可以跳过视频，只看电子书文档。

3D坐标系

在Three.js中进行数学几何空间计算，有必要熟悉和掌握threejs的坐标系特征，下面先复习下基础课程 (opens new window)中关于坐标系的介绍。

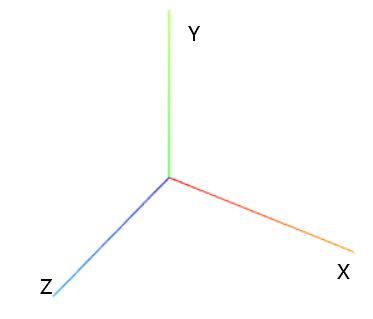
Three.js默认坐标系一个默认y轴向上的右手坐标系 (opens new window)，x轴水平向右，z轴垂直Canvas画布向外。

创建辅助坐标轴THREE.AxesHelper

你可以在threejs代码中创建一个三维辅助坐标系THREE.AxesHelper，用于辅助观察三维场景。

//辅助观察的坐标系
const axesHelper = new THREE.AxesHelper(100);
scene.add(axesHelper);

Threejs坐标系X、Y、Z轴分别对应的颜色是R、G、B，也就是红、绿、蓝。

调整相机视线，观察坐标轴AxesHelper渲染效果

// 位置x、y、z都大于0，视线指向坐标原点
camera.position.set(292, 223, 185);
camera.lookAt(0, 0, 0);

//视线沿着z轴负方向
camera.position.set(x, y, z+400);
camera.lookAt(x, y, z);

//视线沿着z轴正方向
camera.position.set(x, y, z-400);
camera.lookAt(x, y, z);

//视线沿着y轴负方向
camera.position.set(x, y+400, z);
camera.lookAt(x, y, z);

坐标系角度值

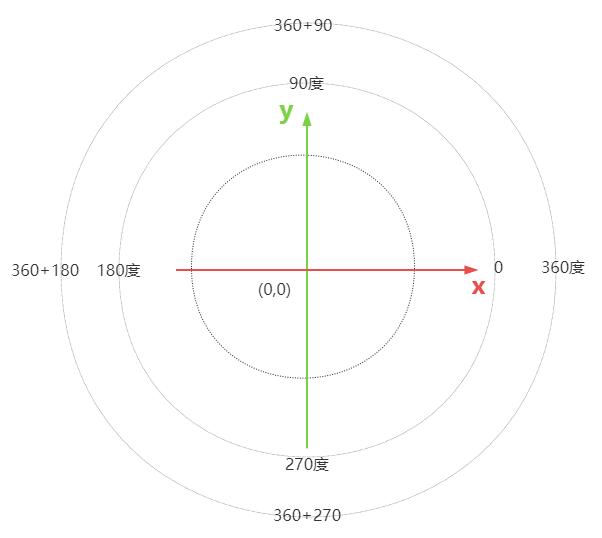
以XOY平面的xoy坐标坐标系为例说明。

以x轴正半轴为起点，作为角度的0度，逆时针旋转一圈是360度，转两圈就是720度，以此类推。

弧度

JavaScript语言里面用Math.PI表示180度对应的弧度值。

console.log('Math.PI',Math.PI);

const angle = Math.PI/6;//30度
const angle = Math.PI/2;//90度
const angle = Math.PI;//180度

MathUtils类度和弧度转换方法

three.js的数学工具类MathUtils也提供度和弧度转化的公式。

// 弧度转度
const angle = THREE.MathUtils.radToDeg(Math.PI);
console.log('Math.PI',angle);

// 度转弧度
const angle = THREE.MathUtils.degToRad(30);

JavaScript三角函数

JavaScript语言Math对象提供了多个用于三角函数计算的方法。

方法	含义
Math.sin(弧度)	正弦值
Math.cos(弧度)	余弦值
Math.tan(弧度)	正切值
Math.asin(正弦值)	反正弦值
Math.acos(余弦值)	反余弦值

三角函数计算点位置

直角坐标中，已知一个点距离坐标原点的长度，和与v轴正半轴夹角，计算改点的x和y坐标。

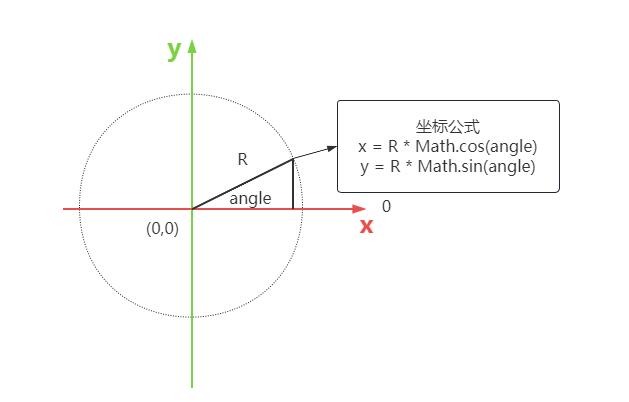
在threejs代码中创建一个球体网格模型可视化表示该点的坐标(x,y)

const R = 100;//半径长度
const angle = Math.PI/6;//30度
// const angle = Math.PI/2;//90度
// const angle = Math.PI;//180度
const x = R * Math.cos(angle);
const y = R * Math.sin(angle);
const geometry = new THREE.SphereGeometry(3); 
const material = new THREE.MeshLambertMaterial({color: 0x00ffff}); 
const mesh = new THREE.Mesh(geometry, material); 
mesh.position.set(x,y,0);

学习方法总结

以后自己学习或探索threejs几何空间计算规律的时候，可以用threejs可视化方式表示出来你的计算结果，这样方便验证自己想法是否正确。比如正弦和余弦值区别，你记不清了，你可以代码测试下。

你可以对比threejs代码中下面两种写法，小球的位置差异，就能判断那个是错误的。

const x = R * Math.cos(angle);
const y = R * Math.sin(angle);

const x = R * Math.sin(angle);
const y = R * Math.cos(angle);

练习题：沿着圆弧批量创建多个小球

你可以尝试利用刚刚介绍的三角函数的知识，在XOY平面上，沿着0~180度半个圆弧等间距创建11个小球。

const R = 100; //圆弧半径
const N = 10; //分段数量
const sp = Math.PI / N; //两个相邻点间隔弧度
const group = new THREE.Group();
for (let i = 0; i < N + 1; i++) {
    const angle = sp * i;
    // 以坐标原点为中心，在XOY平面上生成圆弧上的顶点数据
    const x = R * Math.cos(angle);
    const y = R * Math.sin(angle);
    const mesh = new THREE.Mesh(geometry, material); 
    mesh.position.set(x,y,0);
    group.add(mesh);
}