点乘判断是否在扇形内

通过three.js向量Vector3点乘方法.dot()判断一个点(物体)是否在人前方的扇形范围内。

已知条件

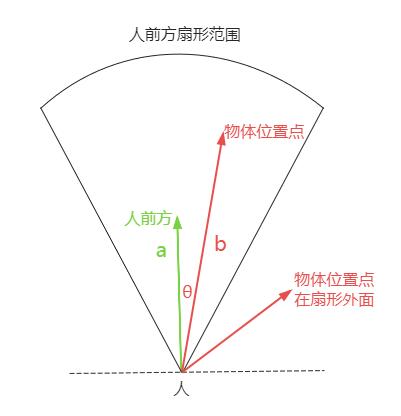
判断一个点(物体)是否在人前方扇形范围内(半径R、扇形角度angle)。

// 已知数据
person.position.set(0, 0, 2);//人位置
mesh.position.set(2, 0, -3);//物体位置
// a向量：人的正前方沿着z轴负半轴
const a = new THREE.Vector3(0, 0, -1);
// 扇形范围
const R = 20;//人前方扇形半径
const angle = 60;//人前方扇形角度

先通过人与物体距离排除，物体不在扇形范围内情况

计算物体与人的距离

// 物体坐标减去人坐标，创建一个人指向物体的向量
const b = mesh.position.clone().sub(person.position);
const L = b.length();//物体与人的距离

比较距离L与扇形半径的关系，排除物体不在扇形范围内的情况。

if (L < R) {//物体与人的距离在半径R以内
    console.log('物体与人距离小于扇形半径');
}else{
    console.log('不在扇形区域内');
}

角度θ在0 ~ 180度余弦值规律

上节课给大家总结过，人指向物体的向量b和表示人正前方的向量a加载在0~180度之间

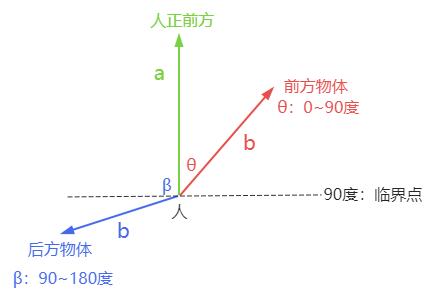
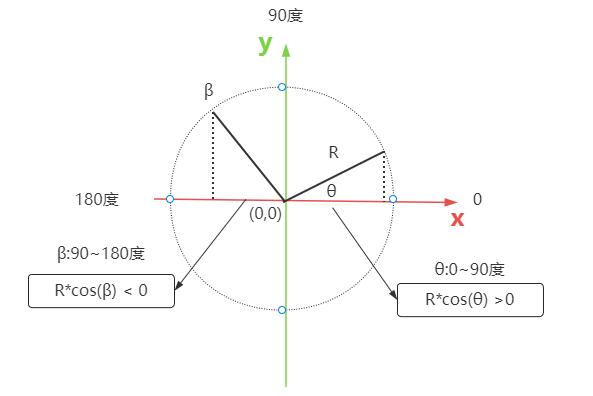
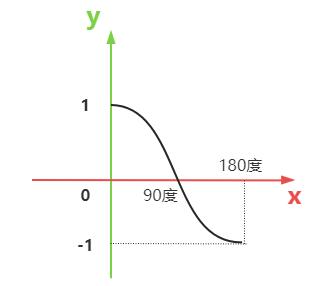
角度θ在0 ~ 180度范围内，随着θ度数的增加，角度θ余弦值 (opens new window)cos(θ)下降。换句话说，向量b与向量a夹角越小，对应的余弦值越大。

比较夹角余弦值大小判断物体是否在扇形内

向量点乘a.dot(b)点乘计算向量a和b的夹角余弦值cos。

b.normalize();//归一化
const cos = a.dot(b);//向量a和b夹角余弦值

在扇形范围内，从人所在位置，向外沿着扇形半径方向绘制向量c，你会发现向量c与向量a最大夹角就是扇形角度一半。

// 角度转弧度
const rad = THREE.MathUtils.degToRad(angle);
// 扇形角度一半的余弦值
const rangeCos = Math.cos(rad / 2)

比较向量a、b夹角余弦值cos和扇形角度一半的余弦值rangeCos大小，判断物体是否在扇形内。

if (L < R) {
    if (cos > rangeCos) {//物体在人前方扇形里面
        console.log('cos',cos);
        console.log('人在半径为R，角度为angle的扇形区域内');
    }else{
        console.log('不在扇形区域内');
    }
}else{
    console.log('不在扇形区域内');
}