叉乘计算三角形法线

利用前面讲解的threejs叉乘.cross()知识，做一个练习题，具体内容就是计算三角形的法线或说着垂线。

已知条件

const geometry = new THREE.BufferGeometry();
// 两个三角形的顶点坐标
const vertices = new Float32Array([
    0, 0, 0, //顶点1坐标
    50, 0, 0, //顶点2坐标
    0, 100, 0, //顶点3坐标
    0, 0, 10, //顶点4坐标
    0, 0, 100, //顶点5坐标
    50, 0, 10, //顶点6坐标
]);
geometry.attributes.position = new THREE.BufferAttribute(vertices, 3);

叉乘.cross()计算法线

通过前面叉乘学习，咱们知道，向量a、b叉乘得到的向量c，会垂直于向量a和b构成的平面。

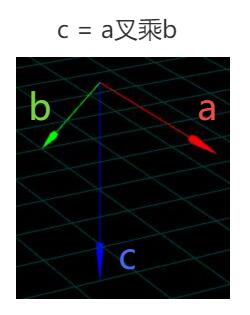
思路非常简单，可以把通过三角形的三个顶点构建两个向量，两个向量叉乘，就会得到一个垂直三角形的向量c。不过注意一点，如果两个向量，随意构建，实际计算结果向量c虽然都垂直a和b但是方向可能有两种情况。所以，三个顶点构建两个向量，按照三角形顶点的顺序，构建1指向2的向量，2指向3的向量,这样可以向量叉乘结果可以反应三角形三个点位置顺序关系。

// 已知三角形三个顶点的坐标，计算三角形法线方向
const p1 = new THREE.Vector3(0, 0, 0);
const p2 = new THREE.Vector3(50, 0, 0);
const p3 = new THREE.Vector3(0, 100, 0);

// 三个顶点构建两个向量，按照三角形顶点的顺序，构建1指向2的向量，2指向3的向量
const a = p2.clone().sub(p1);
const b = p3.clone().sub(p2);

const c = a.clone().cross(b);
c.normalize();//向量c归一化表示三角形法线方向

// 可视化向量a和b叉乘结果：向量c
const arrow = new THREE.ArrowHelper(c, p3, 50, 0xff0000);
mesh.add(arrow);

第二组三角形数据测试法线计算

const p1 = new THREE.Vector3(0, 0, 10);
const p2 = new THREE.Vector3(0, 0, 100);
const p3 = new THREE.Vector3(50, 0, 10);