点乘判断平行向量方向异同

本节课做一个点乘相关的练习题，就是通过three.js点乘方法.dot()判断两个平行的向量，方向是相同还是不同的。

已知条件

// 已知条件：判断两个平行的向量方向是否相同
const a = new THREE.Vector3(10, 0, 0);
const b = new THREE.Vector3(200, 0, 0);//与a平行且方向相同
const b = new THREE.Vector3(-50, 0, 0);//与a平行且方向相反

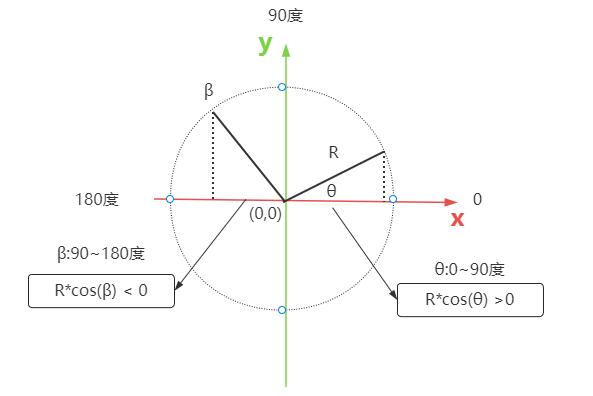
夹角余弦值与向量

两个平行向量方向相同，意味着夹角0度，夹角余弦值cosθ等于1。

两个平行向量方向相反，意味着夹角180度，夹角余弦值cosθ等于-1。

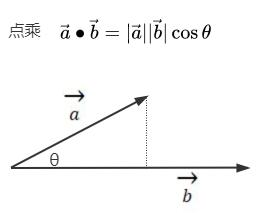
知识点回顾

假设两个向量的夹角是θ，两个向量的单位向量进行点乘.dot()，返回的结果就是夹角θ的余弦值cos(θ)

const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);
// a、b向量归一化后点乘
const cos =  a.normalize().dot(b.normalize());
console.log('向量夹角余弦值',cos);

通过点乘判断平行向量方向异同

// a、b向量归一化后点乘
const cos =  a.normalize().dot(b.normalize());

//注意判断的前提是，两个向量是平行的，余弦值要么1，要么-1
if(cos>0.5){
    console.log('方向相同');
}else{
    console.log('方向相反');
}