Three.js矩阵Matrix4

前面两节课，给大家介绍了模型矩阵的数学基础理论，下面给大家介绍Three.js的一个矩阵相关类Matrix4(4x4矩阵)，并用Matrix4创建平移矩阵、旋转矩阵、缩放矩阵。

查看4x4矩阵Matrix4文档，你可以看到很多相关矩阵相关的数学几何计算方法。

创建4x4矩阵Matrix4对象

// 创建一个4x4矩阵对象
const mat4 = new THREE.Matrix4()

属性.elements设置平移矩阵

通过4x4矩阵Matrix4的属性.elements设置矩阵的值，比如设置一个平移矩阵。

.elements属性值是一个数组，数组的元素就是4x4矩阵的16个数字，数字在数组中按照矩阵列的顺序，一列一节输入数组中。

// 平移矩阵，沿着x轴平移50
// 1, 0, 0, x,
// 0, 1, 0, y,
// 0, 0, 1, z,
// 0, 0, 0, 1
const mat4 = new THREE.Matrix4()
mat4.elements=[1,0,0,0, 0,1,0,0, 0,0,1,0, 50, 0, 0, 1];

.elements属性不设置，默认是单位矩阵。

const mat4 = new THREE.Matrix4()
// 默认值单位矩阵
// 1, 0, 0, 0,
// 0, 1, 0, 0,
// 0, 0, 1, 0,
// 0, 0, 0, 1
console.log('.elements默认值', mat4.elements);

顶点坐标进行矩阵变换Vector3.applyMatrix4()

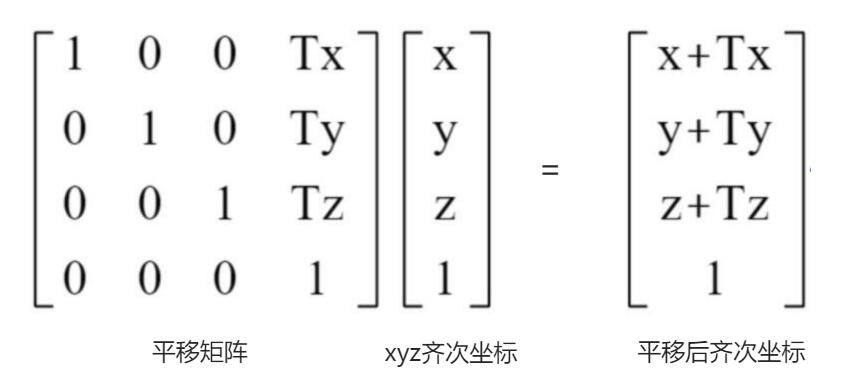
.applyMatrix4()是三维向量Vector3的一个方法，如果Vector3表示一个顶点xyz坐标，Vector3执行.applyMatrix4()方法意味着通过矩阵对顶点坐标进行矩阵变换，比如平移、旋转、缩放。

// 空间中p点坐标
const p = new THREE.Vector3(50,0,0);
// 矩阵对p点坐标进行平移变换
p.applyMatrix4(mat4);
console.log('查看平移后p点坐标',p);

//用小球可视化p点位置
mesh.position.copy(p);

快速生成平移、旋转、缩放矩阵

使用threejs平移矩阵、旋转矩阵、缩放矩阵，可以不用自己直接设置.elements的值。threejs提供了一些更为简单的方法，辅助创建各种几何变换矩阵。

你可以分别测试下面方法，作为练习，去改变一个坐标点，并用小球可视化变换后的坐标位置。

• 平移矩阵.makeTranslation(Tx,Ty,Tz)
• 缩放矩阵.makeScale(Sx,Sy,Sz)
• 绕x轴的旋转矩阵.makeRotationX(angleX)
• 绕y轴的旋转矩阵.makeRotationY(angleY)
• 绕z轴的旋转矩阵.makeRotationZ(angleZ)

const mat4 = new THREE.Matrix4();
// 生成平移矩阵(沿着x轴平移50)
mat4.makeTranslation(50,0,0);
// 结果和.elements=[1,0,0,0,...... 50, 0, 0, 1]一样
console.log('查看矩阵的值',mat4.elements);

平移矩阵案例

const mat4 = new THREE.Matrix4();
// 生成平移矩阵(沿着x轴平移50)
// mat4.makeTranslation(50,0,0);
console.log('查看矩阵的值',mat4.elements);

旋转矩阵案例

const mat4 = new THREE.Matrix4();
//生成绕z轴旋转90度的矩阵
mat4.makeRotationZ(Math.PI/2);