点乘练习-计算三角形夹角

上节课给介绍过threejs向量点乘方法.dot()，下面就应用点乘知识点，做一个案例练习，就是计算一个三角形的夹角角度值。

已知三角形

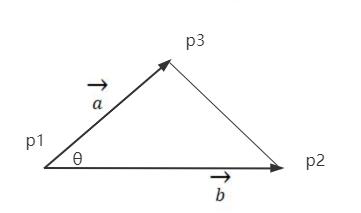
已知三角形三个顶点的坐标，计算其中一个顶点p1对应角度余弦值。

// 三角形的三个点坐标p1，p2，p3
const p1 = new THREE.Vector3(0,0,0);// 点1坐标
const p2 = new THREE.Vector3(20,0,0);// 点2坐标
const p3 = new THREE.Vector3(10,10,0);// 点3坐标

三角形两条边构建向量

目标是计算p1点对应的角度值，所以使用另外两点p2、p3分别与点p1构建向量。

// p1，p3两个点确定一个向量
const a = p3.clone().sub(p1);
// p1，p2两个点确定一个向量
const b = p2.clone().sub(p1);

单位向量点乘.dot()计算夹角余弦值

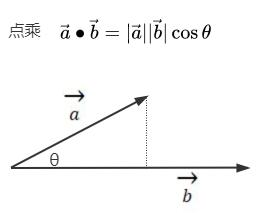
利用上节课的结论，向量a、b归一化.normalize()变成单位向量后，再进行点乘.dot()，结果就是向量a和b夹角对应余弦值。

// a、b向量归一化后点乘
const cos =  a.normalize().dot(b.normalize());

夹角余弦值转角度值

//反余弦计算向量夹角弧度
const rad = Math.acos(cos);
// 弧度转角度
const angle = THREE.MathUtils.radToDeg(rad);
console.log('向量夹角角度值',angle);

注意向量方向对夹角计算的影响

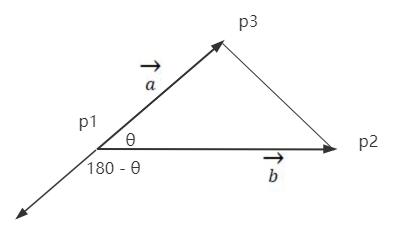
原来向量a和b的夹角45度

const a = p3.clone().sub(p1);//与b夹角45度
const b = p2.clone().sub(p1);

改变向量p1、p3减法顺序，也就是使用p1.clone().sub(p3)代替原来p3.clone().sub(p1)，这样向量a就该变为相反的方向，重新计算角度值，a和b的夹角从45度变为135度。

const a = p1.clone().sub(p3);//与b夹角135度
const b = p2.clone().sub(p1);

如果向量a和b反向都反过来，计算结果还是45度

const a = p1.clone().sub(p3);//与b夹角45度
const b = p1.clone().sub(p2);