判断两个点是否在线段同一侧

通过叉乘.cross()、点乘.dot()综合判断两个点是否在线段同一侧。

已知条件

下面所有点的坐标都在XOZ平面上。

// 已知条件
// 一条线段两点坐标A、B
const A = new THREE.Vector3(0, 0, 10);
const B = new THREE.Vector3(100, 0, 10);

// 判断p1、p2两点位于线段AB同一侧，还是异侧
const p1 = new THREE.Vector3(20, 0, 40);
const p2 = new THREE.Vector3(80, 0, 40);//与p1同侧

const p2 = new THREE.Vector3(80, 0, -30);//与p1异侧

可视化表示出来四个点的坐标和线段

实际开发，为了方便查看几何关系，可以尝试可视化表示一些数据，便于观察，课件源码演示文件中已经提前准备好。

// 小球可视化四个坐标点
const group = new THREE.Group();
const AMesh = createSphereMesh(0xffff00,2);
AMesh.position.copy(A);
const BMesh = createSphereMesh(0xffff00,2);
BMesh.position.copy(B);
const p1Mesh = createSphereMesh(0xff0000,2);
p1Mesh.position.copy(p1);
const p2Mesh = createSphereMesh(0xff0000,2);
p2Mesh.position.copy(p2);
group.add(AMesh,BMesh,p1Mesh,p2Mesh);

function createSphereMesh(color,R) {
    const geometry = new THREE.SphereGeometry(R);
    const material = new THREE.MeshLambertMaterial({
        color: color,
    });
    const mesh = new THREE.Mesh(geometry, material);
    return mesh;
}

// Line可视化线段AB
const geometry = new THREE.BufferGeometry(); 
const vertices = new Float32Array([
    A.x, A.y, A.z, 
    B.x, B.y, B.z, 
]);
geometry.attributes.position = new THREE.BufferAttribute(vertices, 3);
const material = new THREE.LineBasicMaterial({
    color: 0xffff00, 
});
const line = new THREE.LineLoop(geometry, material); 
group.add(line);

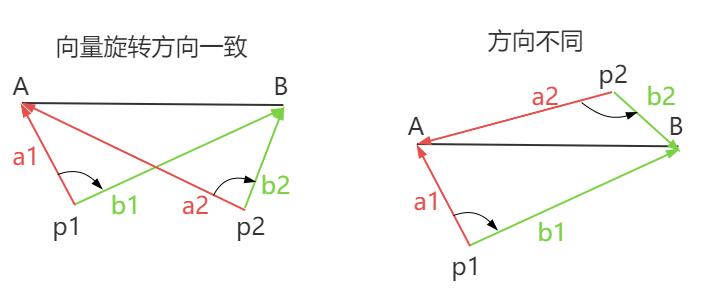
思路讲解

p1分别向线段AB两点创建两条向量a1、b1

p2分别向线段AB两点创建两条向量a2、b2

你会发现，p1、p2同侧时候，a1转向b1与a2转向b2方向一致，如果是异侧，方向不一致。

换句话说，a1叉乘b1得到向量c1，与a2叉乘b2得到向量c2，如果p1、p2同侧，那么c1和c2方向一样，否则方向不同。

总结，这意味着我们可以通过叉乘方向是否相同来推断两点是否位于线段同一侧。

叉乘计算向量c1、c2

// p1分别向线段AB两点创建两条向量a1、b1
const a1 = A.clone().sub(p1);
const b1 = B.clone().sub(p1);
// p2分别向线段AB两点创建两条向量a2、b2
const a2 = A.clone().sub(p2);
const b2 = B.clone().sub(p2);

// 通过c1、c2方向是否相同来推断两点是否位于线段同一侧
const c1 = a1.clone().cross(b1);
const c2 = a2.clone().cross(b2);

箭头可视化所有向量辅助判断

箭头ArrowHelper可视化所有向量，辅助判断，更具体。

group.add(new THREE.ArrowHelper(a1.clone().normalize(), p1, a1.length(),0xff0000))
group.add(new THREE.ArrowHelper(b1.clone().normalize(), p1, b1.length(),0x00ff00))
group.add(new THREE.ArrowHelper(a2.clone().normalize(), p2, a2.length(),0xff0000))
group.add(new THREE.ArrowHelper(b2.clone().normalize(), p2, b2.length(),0x00ff00))
group.add(new THREE.ArrowHelper(c1.clone().normalize(), p1, 50, 0x0000ff))
group.add(new THREE.ArrowHelper(c2.clone().normalize(), p2, 50, 0x0000ff))

判断向量c1、c2方向异同

参考上节课内容讲解

// 向量c1与c2夹角余弦值：用来推断向量c1与c2方向是否相同
const cos =  c1.normalize().dot(c2.normalize());
if(cos>0.5){//方向相同时候，余弦值1>0.5
    console.log('方向相同，两点在线段同侧');
}else{//方向相反时候，余弦值-1<0.5
    console.log('方向相反，两点在线段异侧');
}