数学基础(平移、旋转、缩放矩阵)

本下节课给大家介绍下矩阵的概念，以及用于几何变换的矩阵，比如平移矩阵、缩放矩阵、旋转矩阵。

如果你对这些几何变换的矩阵概念比较熟悉，可以跳过本节课。

线性代数、图形学

如果你有《线性代数》、《计算机图形学》基础，更有利于WebGPU的学习。当然了，你没有这些基础，也没关系，咱们课程的特色就是尽量弱化对数学和图形学基础的要求，尽量带你从零入门。

如果你时间比较充足，也有兴趣，可以去翻翻《线性代数》、《计算机图形学》相关的书籍，当然你不去翻，咱们的课程你也能学习。

如果你数学基础不好，工作也不用封装3D引擎或数学库，可以不用学习《线性代数》，直接用下节课介绍的一个数学库即可。

本节课针对学员

• 大学学过线性代数的矩阵，但是并不了解用于平移、旋转、缩放的矩阵
• 没学过线性代数，数学停留在高中水平

矩阵、矩阵运算规则

矩阵 (opens new window)是图形学中一个比较重要的数学工具。

m×n矩阵表示m行n列的矩阵。

矩阵乘法运算规则 (opens new window)

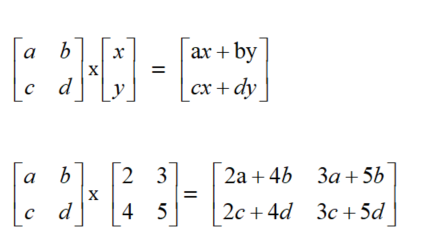
平移矩阵

下面咱们不会严格逻辑推导数学公式，用不严谨的小白方式，给大家介绍下平移矩阵。

一个点的坐标是(x,y,z),假设沿着X、Y、Z轴分别平移Tx、Ty、Tz，毫无疑问平移后的坐标是(x+Tx,y+Ty,z+Tz)。

坐标是(x,y,z)转化为齐次坐标坐标是(x,y,z,1),可以用4x1矩阵表示，这种特殊形式，也可以称为列向量，在webgpu顶点着色器代码中也可以用四维向量vec4表示。

请用矩阵的乘法运算法则验证下面矩阵的等式是否成立?

缩放矩阵

通过缩放矩阵可以对顶点的齐次坐标进行缩放。

旋转矩阵

假设一个点的坐标是(x,y,z),经过旋转变换后的坐标为(X,Y,Z)

绕Z轴旋转γ角度,z的坐标不变不变，x、y的坐标发生变化，如果你有兴趣，可以用你高中的三角函数知识推理，可以知道旋转后的坐标：X=xcosγ-ysinγ,Y=xsinγ+ycosγ

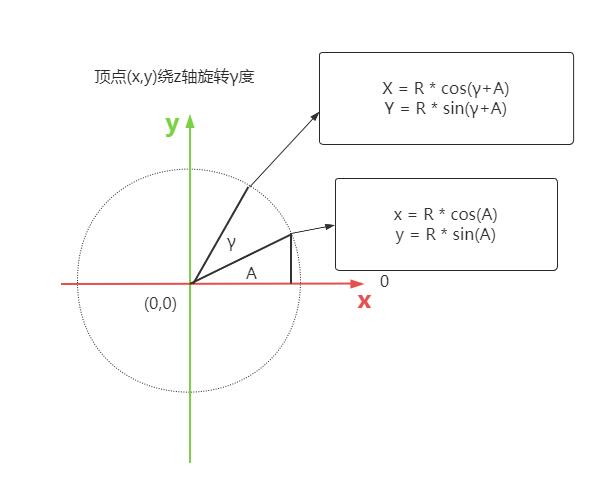
三角函数计算推理过程

// 假设旋转前角度A，对应x和y的值
x = R * cos(A)
y = R * sin(A)

// 假设旋转了γ度，对应X和Y的值
X = R * cos(γ+A)
  = R * (cos(γ)cos(A)-sin(γ)sin(A))
  = R*cos(A)cos(γ) - R*sin(A)sin(γ)
  = xcosγ-ysinγ

Y = R * sin(γ+A)
  = R * (sin(γ)cos(A)+cos(γ)sin(A))
  = R*cos(A)sin(γ) + R*sin(A)cos(γ)
  = xsinγ+ycosγ

旋转后的坐标：X=xcosγ-ysinγ,Y=xsinγ+ycosγ

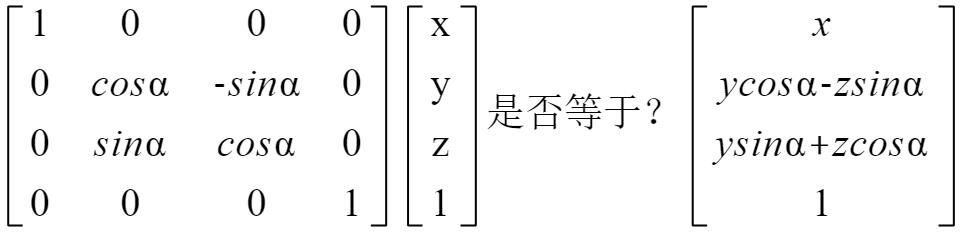
绕X轴旋转α角度

x的坐标不变，y、z的坐标发生变化，Y=ycosα-zsinα,Z=ysinα+zcosα

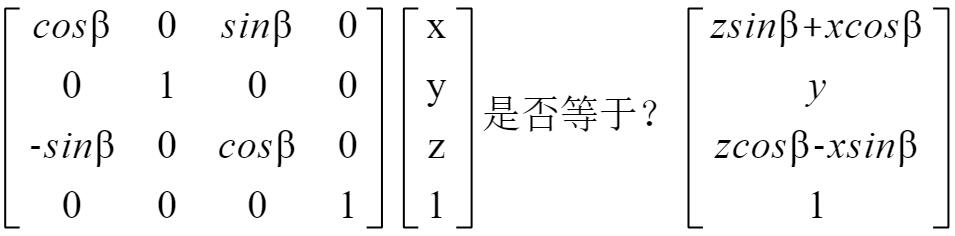
绕Y轴旋转β角度

y的坐标不变，z、x的坐标发生变化，Z=zsinβ+xcosβ,X=zcosβ-xsinβ